سودوکو روزانه میلیونها نفر در سراسر جهان را با معماهای پیچیده خود سرگرم می کند. با این حال، حتی حرفهایترین افرادی که این معماها را حل میکنند، ممکن است از وجود یک الگوی پنهانی که در تمام سودوکوها وجود دارد، بیخبر باشند.
ریاضیدانان به تازگی الگویی به نام «حلقه فیستومفل» را کشف کردهاند که در همه سودوکوها وجود دارد. نکته جالب این است که این الگو میتواند به حل سریعتر معماهای دشوار سودوکو کمک کند.
این نشان میدهد که ۱۶ مربع اطراف حلقه مرکزی ۳×۳، همان اعدادی را در خود دارند که در چهار مربع ۲×۲ گوشههای جدول قرار گرفتهاند.
از آنجایی که این ویژگی در همه سودوکوهای استاندارد وجود دارد، میتوان از آن برای معماهایی که حلشان غیرممکن به نظر میرسد، استفاده کرد.
به گفته پروفسور سارا هارت، ریاضیدان دانشگاه بیرکبک لندن و نویسنده کتاب «روزی روزگاری یک عدد اول»، آگاهی از این مجموعههای معادل میتواند در حل معماهای دشوار بسیار کمککننده باشد.
اگر در سودوکوی بعدی خود از این الگو استفاده کنید، حل کردن معما سادهتر خواهد شد.
در سودوکو، یک جدول ۹×۹ باید با اعداد ۱ تا ۹ پر شود. شرط اصلی این است که هر ردیف، هر ستون و هر بلوک ۳×۳ شامل تمام اعداد ۱ تا ۹ باشد و هیچ عددی تکرار نشود.
رعایت این قوانین باعث میشود که حل سودوکو چالشبرانگیز باشد. اما همین قوانین، الگوهای ریاضی جالبی را ایجاد میکنند که میتوان از آنها استفاده کرد.
«حلقه فیستومفل» نمونهای از مفهومی به نام «نظریه معادلسازی مجموعهها» است. پروفسور هارت توضیح میدهد که در هر جدول سودوکو، برخی از خانهها باید حاوی مجموعه یکسانی از اعداد باشند. بهطور مثال، هر ردیف، هر ستون و هر بلوک ۳×۳ شامل اعداد ۱ تا ۹ هستند که این موضوع مجموعههایی معادل را تشکیل میدهد.
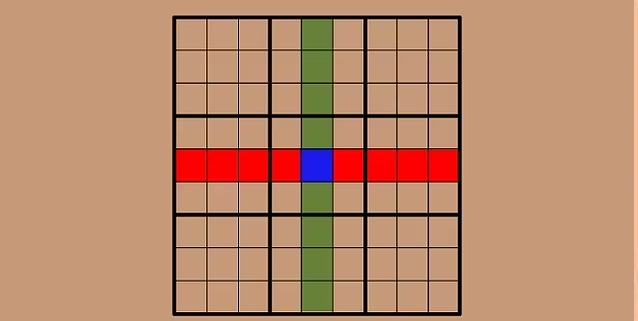
در ویدیویی از یوتیوبر Numberphile نشان داده شده که ستون و ردیف مرکزی هر سودوکو باید شامل مجموعهای از همان اعداد باشند.
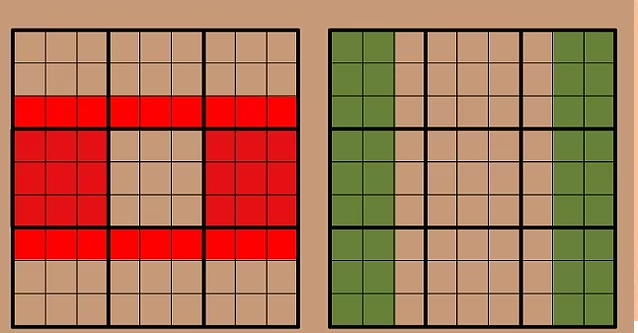
اگرچه ترتیب این اعداد ممکن است مشخص نباشد، اما هر دو شامل اعداد ۱ تا ۹ خواهند بود.
این مفهوم زمانی جالبتر میشود که ببینیم این مجموعهها در نقاطی با هم همپوشانی دارند.
برای مثال، ستون و ردیف مرکزی در یک مربع مشترک – یعنی مربع مرکزی جدول – همپوشانی دارند.
حتی اگر مقدار این مربع مشخص نباشد، عدد آن در هر دو مجموعه تأثیر یکسانی دارد.
اگر این مربع حذف شود، عدد آن از هر دو مجموعه کم میشود و مجموعهها همچنان معادل باقی میمانند.
برای نمونه، اگر مربع مرکزی عدد «۹» باشد، با حذف آن، هر دو مجموعه همچنان اعداد ۱ تا ۸ را شامل خواهند بود.
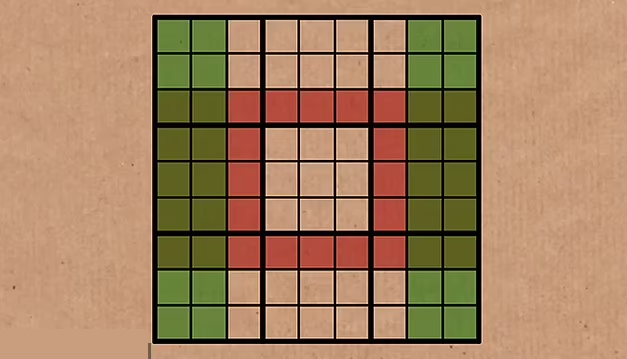
این ایده زمانی سودمندتر میشود که متوجه شویم مجموعههای بزرگتری هم وجود دارند که دارای همپوشانی بیشتری هستند.
حلقه فیستومفل نمونهای از این مجموعههای معادل است که تقارن زیبایی دارد و درک آن کمی پیچیدهتر است.
این الگو با دو ستون سمت راست و چپ جدول شروع میشود و سپس به دو بلوک ۳×۳ در سمت چپ و راست بلوک مرکزی و ردیفهای بالای آن گسترش مییابد.
براساس قوانین سودوکو، هر یک از این مجموعهها شامل چهار گروه از اعداد ۱ تا ۹ هستند که به ترتیبی خاص چیده شدهاند.
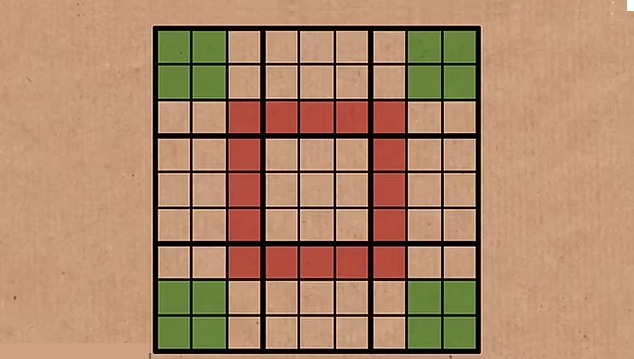
هر نقطه همپوشانی بین این مجموعهها همان عدد را در هر دو مجموعه ایجاد میکند.
با حذف مربعهای همپوشان، یک حلقه مرکزی شامل ۱۶ مربع و چهار مربع ۲×۲ در گوشهها باقی میماند که باید شامل اعداد یکسانی باشند.
ویژگی جذاب این الگو این است که بدون توجه به ترتیب اعداد، همیشه صادق است. حتی اگر بهجای اعداد، سودوکو با ایموجیها یا حروف پر شود، این قاعده همچنان برقرار است.
حلقه فیستومفل تنها یکی از نمونههای مجموعههای معادل در سودوکو است و ریاضیدانان موفق به شناسایی مجموعههای متعددی از این نوع شدهاند.
به گفته پروفسور هارت، دانستن این قوانین میتواند ابزار جدیدی برای افرادی باشد که در حل برخی معماهای پیچیده دچار مشکل شدهاند. او این موضوع را به یادگیری استراتژیهای شطرنج تشبیه کرده و گفته است:
هرچه روشها و تاکتیکهای بیشتری بدانید، گزینههای بیشتری برای مدیریت چالشها خواهید داشت.
